Defining a structural model with lumped dynamics

This tutorial describes how to define a structural model only, in this case for a small electric motor.

Click here for the full script for this tutorial.

Consider an idealized model of an electric motor: 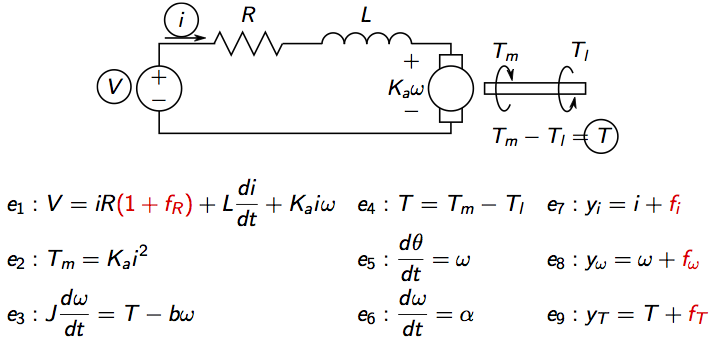where V is voltage, i current, Tm motor torque, Tl load torque, omega rotational speed, theta motor angle. There are four considered faults, three sensor faults and a change in the internal resistance.

One strength of structural analysis is that it can be performed early in the development process, when only coarse details of the model is known. Therefore, only the model structure is assumed known and the values of the parameters R, L, J, Ka, and b are therefore assumed unknown.

To define a model, a model definition is constructed. First, the type of model is defined, here a structural model defined by variable names. This is defined as

modelDef.type = 'VarStruc';

It is possible to define the model structure by indicence matrices directly, but this is prone to errors so we use the variable names instead.

After that, partition the set of variables in three categories; unknown (x), known (z), and faults (f). Here, a lumped model is defined which means that dynamics constraints are treated as algebraic. To explicitly state the differential constraints, see the tutorial where the symbolic model of the electric motor is defined. Then,

modelDef.x = {'I','w','theta','alpha','T','Tm','Tl'};
modelDef.f = {'fR','fi','fw','fT'};
modelDef.z = {'V','yi','yw','yd'};

The next step is to define the structure for all model equations.

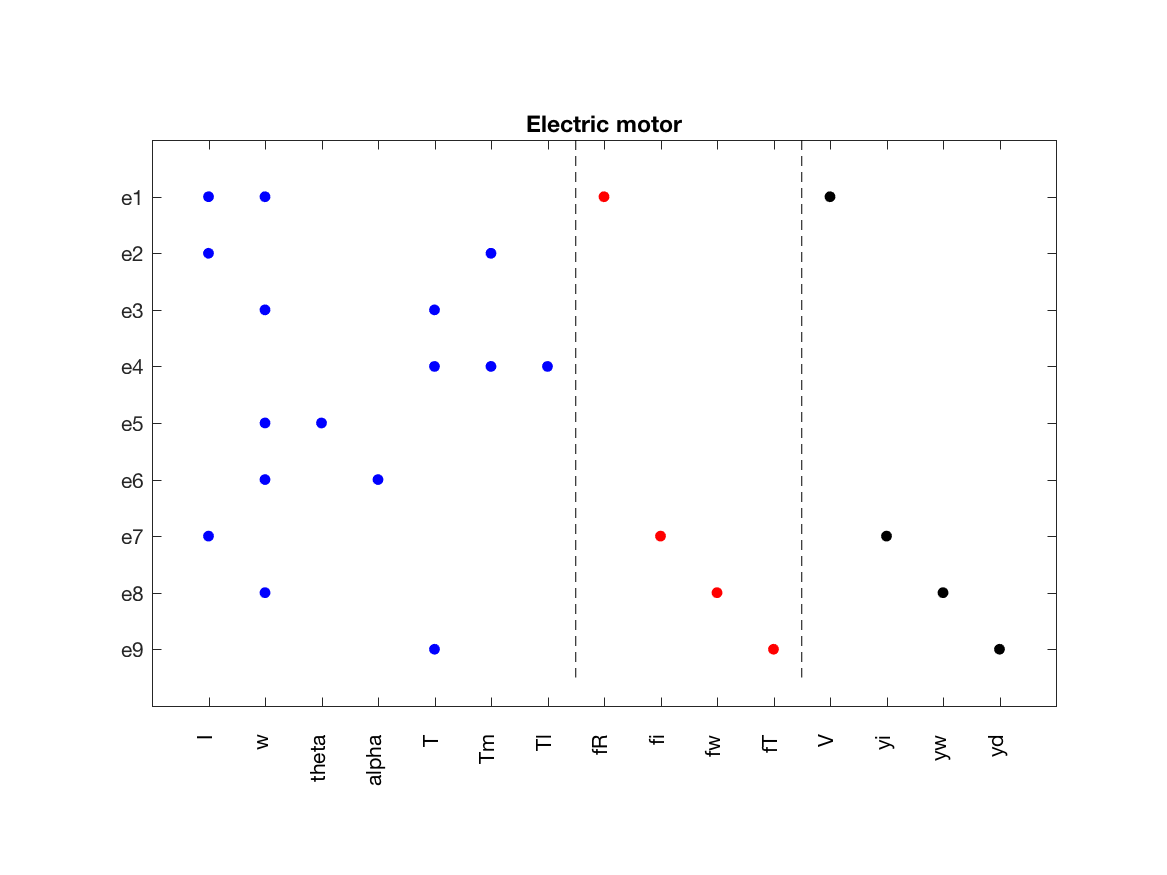
modelDef.rels = {...
  {'V', 'fR', 'I', 'w'}, ... % e1
  {'Tm', 'I'}, ...           % e2
  {'w', 'T'}, ...            % e3
  {'T', 'Tm', 'Tl'}, ...     % e4
  {'theta', 'w'}, ...        % e5
  {'w', 'alpha'}, ...        % e6
  {'yi', 'I', 'fi'}, ...     % e7
  {'yw', 'w', 'fw'}, ...     % e8
  {'yd', 'T', 'fT'}};        % e9

Now, everything is defined and we create the model object and give it a name as

model = DiagnosisModel( modelDef );
model.name = 'Electric motor';

Now, the model is defined and to print some basic model information, use tha class method Lint

>> model.Lint()
Model: Electric motor

  Type: Structural, static

  Variables and equations
    7 unknown variables
    4 known variables
    4 fault variables
    9 equations, including 0 differential constraints

  Degree of redundancy: 2
  Degree of redundancy of MTES set: 1

  Model validation finished with 0 errors and 0 warnings.

And to graphically plot the model structure, use the PlotModel class method

model.PlotModel()

which produces the figure